$\newcommand{\dede}[2]{\frac{\partial #1}{\partial #2} } \newcommand{\dd}[2]{\frac{\mathrm{d} #1}{\mathrm{d} #2}} \newcommand{\divby}[1]{\frac{1}{#1} } \newcommand{\typing}[3][\Gamma]{#1 \vdash #2 : #3} \newcommand{\xyz}[0]{(x,y,z)} \newcommand{\xyzt}[0]{(x,y,z,t)} \newcommand{\hams}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyz} \newcommand{\hamt}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyzt} \newcommand{\ham}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2}) + V(x)} \newcommand{\abs}[1]{\left|\left| #1 \right|\right|} \newcommand{\unit}[1]{\, \mathrm{#1}} \require{mathtools} \newcommand{\abk}[1]{\langle #1 \rangle}$
Morgen 1 - Definitionen & Grundlagen
Geschwindigkeit
- Umsatzgeschwindigkeit: Wie viel Stoffmenge wir pro Zeit umgesetzt:
$$ v^{ums}_i = \frac{1}{\nu_i} \dd{n_i}{t} $$
Dabei ist $\nu_i$ die der stöchiometrische Koeffizient des Stoffes $i$ in der Reaktionsgleichung und $n_i$ die Stoffmenge des Stoffes $i$.
- Reaktionsgeschwindigkeit: Wie schnell die Konzentration eines Stoffes sich ändert:
$$ v^{rnx}_i = \frac{1}{\nu_i} \dd{c_i}{t} $$
- Zusammenhang zwischen Umsatzgeschwindigkeit und Reaktionsgeschwindigkeit:
$$ v_i^{rxn} = v_i^{ums} \cdot \frac{1}{V} $$
Also einfach durchs Volumen $V$ teilen.
Ab hier werden wir $v_i^{rxn}$ als $v_i$ oder sogar nur $v$ schreiben, da wir die Umsatzgeschwindigkeit grundsätzlich nicht benötigen.
Stöchiometrische Koeffizienten
-
Stöchiometrische Koeffizienten sind die Zahlen vor den Stoffen in der Reaktionsgleichung.
-
Mache aus dem Pfeil $\rightarrow$ ein Gleichheitszeichen $=$
- Alles auf die rechte Seite des Gleichheitszeichens schreiben. Die Edukte haben per Konvention ein negatives Vorzeichen.
$$ \begin{aligned} A+B &\rightarrow C+D \\ A+B &= C+D \\ 0 &= -A-B+C+D \end{aligned} $$
Beispiel: Schreibe die Geschwindigkeit der unteren Reaktion auf $$ A+B \rightarrow 2C $$
- Koeffizienten bestimmen:
$$ \nu_A = -1, \nu_B = -1, \nu_C = 2 $$
- Geschwindigkeitsdefinition aufschreiben:
$$ v = - \dd{c_A}{t} = - \dd{c_B}{t} = + \frac{1}{2} \dd{c_C}{t} $$
Geschwindigkeitsgesetze
Diese Form gilt eigentlich nur für Elementarreaktionen, aber wir haben sowieso nur diese in der Vorlesung behandelt:
$$ v = k \cdot c_A^{|\nu_A|} \cdot c_B^{|\nu_B|} \cdot c_C^{|\nu_C|} \cdot ... = k \cdot \prod_{i=1}^n c_i^{|\nu_i|} $$
für eine Reaktion:
$$ \nu_A A + \nu_B B + \dots \rightarrow \dots $$
Es gehen also nur die Konzentrationen der Edukte in das Geschwindigkeitsgesetz! Die Produkte spielen hier keine Rolle.
Kombinieren von Reaktionen
Haben wir nicht mehr eine einfache Reaktion, die nur in eine Richtung geht, sondern z.B. eine Reaktion mit Rückreaktion, so können wir die Geschwindigkeitsgesetze einfach addieren.
Beispiel Rückreaktion
$$ \ce{A + B <=>[k_{-1}]{k_1} C + D} $$
Das können wir auseinanderbauen zu zwei Elementarreaktionen:
$$ \begin{aligned} \ce{A + B &->[$k_1$] C + D} \\ \ce{C + D &->[$k$_{-1}] A + B} \end{aligned} $$
Schreibe nun zuerst die Geschwindigkeitsgesetze der einzelnen Reaktionen auf:
$$ \begin{aligned} v_1 &= \dd{c_A}{t} &= - k_1 \cdot c_A \cdot c_B \\ v_{-1} &= \dd{c_C}{t} &= - k_{-1} \cdot c_C \cdot c_D \end{aligned} $$
Nun addieren wir die Geschwindigkeitsgesetze, wobei wir die Geschwindigkeiten der Rückreaktion mit einem Minuszeichen versehen:
$$ \dd{c_A}{t} = v_1 - v_{-1} = - k_1 \cdot c_A \cdot c_B + k_{-1} \cdot c_C \cdot c_D $$
Intuitiv: Die Geschwindigkeit der Rückreaktion ist proportional zur Konzentration der Produkte, die Geschwindigkeit der Vorwärtsreaktion ist proportional zur Konzentration der Edukte.
Beispiel Konkurrenzreaktion
$$ \begin{aligned} \ce{A + B &->[k_1] C} \\ \ce{2A &->[k_2] D} \end{aligned} $$
Auch hier stellen wir die einzelnen Geschwindigkeitsgesetze auf:
$$ \begin{aligned} v_1 &= \dd{c_A}{t} = - k_1 \cdot c_A \cdot c_B \\ v_2 &= \frac{1}{2} \dd{c_A}{t} = - k_2 \cdot c_A^2 \end{aligned} $$
Und addieren sie:
$$ \dd{c_A}{t} = v_1 + 2 v_2 = - k_1 \cdot c_A \cdot c_B - 2 k_2 \cdot c_A $$
Nanu, woher kommt der Faktor $2$ bei $k_2$? Die Geschwindigkeit der Reaktion 2 muss doppelt gewichtet werden, da wir zwei Moleküle A verbrauchen!
Beispiel Atomrekombinationen
Bei Atomrekombinationen benötigen wir nicht mehr nur die Edukte, sondern auch einen Stosspartner, damit die Reaktion möglich wird. Sonst haben die Produkte zu viel Energie und zerfallen gleich wieder/entstehen gar nicht wirklich.
$$ \begin{aligned} H+H+H &\xrightarrow{k_1} H_2+H \\ H+H+H &= H_2+H \\ 0 &= -2H + H_2 \\ \end{aligned} $$
Somit finden wir die stöchiometrischen Koeffizienten $-2$ für H und $1$ für $H_2$. Das Geschwindigkeitsgesetz lautet dann:
$$ v = - \frac{1}{2} \dd{c_H}{t} = k_3 \cdot c_H^3 $$
Hier ist es also etwas anders als bei den obigen Reaktionen, da dies keine Elementarreaktion ist. Die Atomreaktion ist aber der einzige in der Vorlesung betrachtete Fall.
Reaktionsordnung
Die Reaktionsordnung ist nur definiert für Reaktionen, die ein Geschwindigkeitsgesetz der Form
$$ v = k \prod_{i=1}^n c_i^{m_i} $$
haben. Die Reaktionsordnung ist dann einfach die Summe der Exponenten:
$$ \sum_{i=1}^n m_i $$
Vorher war $m_i$ immer $|\nu_i|$, aber das gilt nur für Elementarreaktionen! Die Reaktionsordnung ist jedoch eine experimentell bestimmte Grösse und somit können die $m_i$ beliebige (nicht mal unbedingt ganze!) Zahlen sein. Die Reaktionsordnung kann auch nur für einen Stoff definiert sein, falls die Geschwindigkeit nur zu dessen Konzentration proportional ist (siehe Beispiel unten).
Beispiel Ablesen Reaktionsordnung
Betrachten wir das Geschwindigkeitsgesetz
$$ v = k_1 \cdot c_A^2.3 \cdot c_B + k_2 \cdot c_A \cdot c_B $$
So lässt sich nur $c_B$ ausklammern und wir erhalten:
$$ v = c_B \cdot (k_1 \cdot c_A^{2.3} + k_2 \cdot c_A) $$
Damit ist die Reaktionsordnung von $B$ einfach $1$. Die Reaktionsordnung von $A$ ist nicht definiert, da $c_A$ nicht komplett ausgeklammert werden kann.
Molekularität
Definition: Anzahl Teilchen, die beim "essenziellen/wesentlichen" Schritt der Reaktion miteinander interagieren. Wir kennen wie Fälle:
- Unimolekular (Monomolekular)
- Bimolekular
- Trimolekular (Atomrekombinationen)
Beispiel Molekularität
$$ H+H_2O+CO_2 \xrightarrow{k} H_2CO_3 + H $$
Diese Reaktion ist bimolekular, da nur $H_2O$ und $CO_2$ miteinander reagieren. $H$ ist nur ein Stosspartner. Die Ordnung der Reaktion hingegen ist irgendwas zwischen $2$ und $3,$ da $H$ als Stosspartner in das Geschwindigkeitsgesetz eingehen kann.
Aber wie mache ich jetzt das Geschwindigkeitsgesetz? Naja, definiere einfach einen Parameter $m \in [0,1]$ und schreibe das Geschwindigkeitsgesetz auf:
$$ v = - \dd{c_{H2O}}{t} = k \cdot c_{H_2O} \cdot c_{CO_2} \cdot c_H^m = k' \cdot c_{H_2O} \cdot c_{CO_2} $$
mit $k' = k c_H^m$.
Dimension und Einheit von $k$
Die Dimension der Reaktionsgeschwindigkeit $v$ muss immer:
$$ dim(v) = \frac{\text{Konzentration}}{\text{Zeit}} \equiv \frac{\text{mol}}{\text{s} \cdot \text{L}} $$
betragen. Damit dies erfüllt wird, muss die Einheit von $k$ immer:
$$ dim(k) = \frac{\text{Konzentration}}{\text{Zeit} \cdot \text{Konzentration}^m} \equiv \frac{1}{\text{s} \cdot \left( \frac{\text{mol}}{\text{L}} \right)^{m-1}} $$
sein. Die Einheit von $k$ ist also abhängig von der Reaktionsordnung $m$.
Mögliche Bedingungen/Vereinfachungen beim Aufschreiben von Gesetzen
- Überschuss: $[A]_0 \gg [B]_0 \Rightarrow c_A(t) = [A]_0$
- Gleiche Anfangskonzentration:
$$ [A]_0 = [B]_0 \Rightarrow c_A(t) = c_B(t) \Rightarrow v = - \dd{c_A}{t} = k c_A c_B = k c_A^2 $$
Lösen von Geschwindigkeitsgesetzen
Mach dir eine Tabelle auf die Zusammenfassung für die Prüfung!
Beispiel
Betrachte die Reaktion
$$ A+B \xrightarrow{k} \text{Produkte} \qquad \text{ mit } [A]_0 = [B]_0 $$
Finde eine Formel für $c_A(t)$.
1. Schreibe das Geschwindigkeitsgesetz auf:
$$ v = - \dd{c_A}{t} = k \cdot c_A \cdot c_B = k \cdot c_A^2 $$
2. Löse die Differentialgleichung:
$$ \begin{aligned} \dd{c_A}{t} &= - k \cdot c_A^2 \\ \int_{c_A(0)}^{c_A(t)} \frac{1}{c_A^2} \dd{c_A}{t} &= - k \int_0^t \dd{t} \\ \frac{1}{c_A(0)} - \frac{1}{c_A(t)} &= - k t \\ \frac{1}{c_A(t)} &= \frac{1}{c_A(0)} + k t \\ c_A(t) &= \frac{1}{\frac{1}{c_A(0)} + k t} \\ c_A(t) &= \frac{c_A(0)}{1 + k c_A(0) t} \end{aligned} $$
Solche Rechnungen sind unter Prüfungsbedingungen natürlich nicht einfach, deswegen empfehle ich das auf die Zusammenfassung zu klatschen.
Halbwerts-, Lebens- und X-Zeit
Auch hier gehören die Formeln für die verschiedenen Gesetze auf die Zusammenfassung.
Halbwertszeit
Die Halbwertszeit ist die Zeit, die vergeht, bis die Hälfte des Edukts umgesetzt ist. Mathematisch wird das wie folgt ausgedrückt:
$$ c_A(t_{1/2}) = \frac{1}{2} c_A(0) $$
Lebenszeit
Die Lebenszeit ist die Zeit, die vergeht, bis $1/e$ des Edukts umgesetzt ist. Sie wird mit $\tau$ bezeichnet und kann wie folgt ausgedrückt werden:
$$ c_A(\tau) = \frac{1}{e} c_A(0) $$
X-Zeit
Die X-Zeit ist die Zeit, die vergeht, bis $1/X$ des Edukts umgesetzt ist und ist analog zu den obigen definiert.
Radioaktiver Zerfall
Beim radioaktiven Zerfall ist das Geschwindigkeitsgesetz besonders einfach:
$$ v = - \dd{c_A}{t} = k \cdot c_A $$
und die X-Zeit lässt sich direkt ablesen:
$$ t_{1/X} = \frac{\ln(X)}{k} $$
Allgemeinere Formeln
Für eine etwas allgemeinere Reaktion der Form
$$ A+B+C+\dots \xrightarrow{k} \text{Produkte} \qquad \text{ mit } [A]_0 = [B]_0 = [C]_0 = \dots $$
erhalten wir das Geschwindigkeitsgesetz
$$ v = - \dd{c_A}{t} = k \cdot c_A \cdot c_B \cdot c_C \cdot \dots = k \cdot c_A^m $$
wobei $m$ die Reaktionsordnung ist. Die Halbwertszeit beträgt dann:
$$ t_{1/2} = \frac{2^{m-1}-1}{c_0^{m-1} \cdot k \cdot (m-1)} $$
oder in linearisierter Form
$$ \ln(t_{1/2}) = \ln(\frac{2^{m-1}-1}{k\cdot(m-1)}) + (m-1) \ln(c_0) $$
was wir später noch brauchen werden.
Quasistationarität und Vorgelagertes Gleichgewicht
Quasistationarität
Die Quasistationarität ist eine Vereinfachung, die wir machen können, wenn ein Stoff etwa gleich schnell gebildet wie er wieder abgebaut wird. Dann ist die Konzentration des Stoffes in etwa konstant
$$ \dd{c_A}{t} \approx 0 $$
und wir können dies in das Geschwindigkeitsgesetz einsetzen
$$ v = k \cdot \dots \approx 0 $$
Dies ist aber nicht zu verwechseln mit $c_A(t) \approx 0$, die Konzentration des Stoffes $A$ ist nicht null, aber verändert sich nicht.
Vorgelagertes Gleichgewicht
Ein vorgelagertes Gleichgewicht ist eine Situation wie
$$ \begin{aligned} A &\xrightleftharpoons[k_{-1}]{k_1} B \\ B &\xrightarrow{k_2} C \end{aligned} $$
wobei die erste Reaktion im Gleichgewicht ist, d.h. Vor- und Rückreaktion finden gleich schnell statt:
$$ k_1 \cdot c_A = k_{-1} \cdot c_B $$
Dies können wir umformen zu
$$ \frac{k_a}{k_b} = \frac{c_B}{c_A} = K $$
was als Gleichgewichtskonstante $K$ bezeichnet wird. Je nach Situation kann und das weiterhelfen.
Nachmittag 1 - Zustandssummen & TST
Freiheitsgrade
Für ein Molekül aus $N$ Atomen sind die (verschiedenen Arten von) Freiheitsgraden gegeben durch:
| Form | $F_{rot}$ | $F_{vib}$ | $F_{trans}$ | $F_{tot}$ |
|---|---|---|---|---|
| linear | $2$ | $3N-5$ | $3$ | $3N$ |
| nicht-linear | $3$ | $3N-6$ | $3$ | $3N$ |
| Übergangszustand linear | $2$ | $3N-5-1$ | $3$ | $3N-1$ |
| Übergangszustand nicht-linear | $3$ | $3N-6-1$ | $3$ | $3N-1$ |
Im Übergangszustand gibt es einen Freiheitsgrad weniger, da er durch die Festlegung der Reaktionskoordinate 'verbraucht' wurde.
Energie und Zustandssummen
Vibration
Betrachten wir Vibration, so nehmen wir immer einen harmonischen Oszillator an. Die Energie ist dann gegeben durch:
$$ E_{vib,n} = h\nu\left(n+\frac{1}{2}\right) = h c \tilde{\nu}\left(n+\frac{1}{2}\right) $$
wobei $\tilde{\nu} = \frac{1}{2\pi} \sqrt{\frac{k}{\mu}}$ mit der Kraftkonstante $k$ und der reduzierten Masse $\mu$ ist.
Bei Isotopen bleibt $k$ gleich und nur $\mu$ ändert sich. Wir können also die Wellenzahl $\tilde{\nu}$ von einem Isotop zum anderen übertragen:
$$ \tilde{\nu}_1 = \tilde{\nu}_2 \sqrt{\frac{\mu_2}{\mu_1}} $$
Die Zustandssumme ist gegeben durch
$$ q_{vib} = \sum_{n=0}^{\infty} e^{-\beta E_{vib,n}} = \frac{1}{1-e^{-\beta h c \tilde{\nu}}} $$
wobei $\beta = \frac{1}{k_B T}$ (viel schöner als jedes mal $\frac{1}{k_B T}$ zu schreiben).
Rotation
Für die Rotation benutzen wir den starren Körper mit
$$ E_{rot, J} = \frac{\hbar^2}{2I} J(J+1) = h c B J(J+1) $$
wobei $B = \frac{h}{8\pi^2 I}$ die Rotationskonstante (meist direkt gegeben) und $I = \sum_i m_i r_i^2$ das Trägheitsmoment ist. Für zweiatomige Moleküle ist das Trägheitsmoment besonders einfach $I = \mu r^2$ mit $\mu$ der reduzierten Masse $\mu = \frac{m_1 m_2}{m_1+m_2}.$
Für die Zustandssumme ergibt sich dann
$$ q_{rot, \text{linear}} \frac{1}{h c B \beta} $$
$$ q_{rot, \text{nicht-linear}} = \sqrt{\pi} \left(\frac{1}{h c \beta}\right)^{3/2} (A B C)^{-1/2} $$
mit $A, B, C$ Rotationskonstanten, die gegeben werden.
Translation
Die Energie sollte jedem bekannt sein mit
$$ E_{kin} = \frac{1}{2} m v^2 $$
Daraus ergibt sich dann die Zustandssumme
$$ q_{trans} = V \left(\frac{2 \pi m}{h^2 \beta}\right)^{3/2} $$
Elektronische Levels
Das wird gegeben, falls gebraucht. Grundsätzlich befassen wir uns aber mit Energieniveaus, die nicht ausreichen um Elektronen anzuregen, womit die Zustandssumme $q_{el} = 1$ ist und einfach wegfällt.
Gesamtzustandssumme
Die Gesamtzustandssumme ist dann gegeben durch das Produkt der einzelnen Zustandssummen
$$ q_{tot} = q_{vib} q_{rot} q_{trans} q_{el} (q_{\text{Kernspin}} \sigma^{-1}) $$
wobei die beiden letzten Terme nur relevant sind, falls sich der Kernspin ändert oder das Molekül eine Symmetrieachse hat. In diesem Fall wird euch das aber gesagt, das müsst ihr nicht selbst herausfinden.
Übergangszustandstheorie (Transition State Theory)
Setzen wir die Energie des Zustandes eines Moleküls während einer Reaktion der Reaktionskoordinate $r$ gegenüber, so erhalten wir eine Born-Oppenheimer Potentialkurve
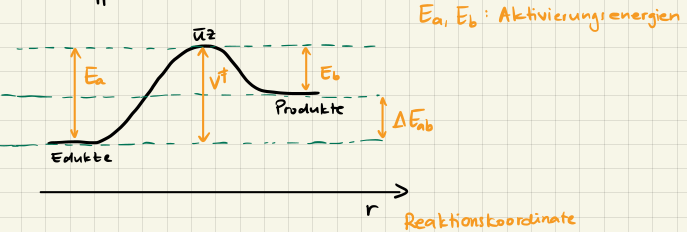
Die Reaktionskoordinate $r$ ist dabei eine fiktive Koordinate, die den Fortschritt der Reaktion beschreibt. Der Übergangszustand ist der Punkt auf der Potentialkurve, an dem die Energie maximal ist und die Energiedifferenz zwischen dem Übergangszustand (ÜZ) und dem Ausgangszustand ist die Aktivierungsenergie $E_a$.
Nach der ÜZ-Theorie ist die Geschwindigkeitskonstante $k$ gegeben durch
$$ \begin{aligned} k_{uni} &= \frac{1}{h \beta} \frac{q^{\ddagger}}{q_{E}} e^{-\beta E_a} \\ k_{bi} &= \frac{1}{h \beta} \frac{q^{\ddagger}}{q_{E_1} q_{E_2}} e^{-\beta E_a} \end{aligned} $$
wobei $q^{\ddagger}$ die Zustandssumme des Übergangszustandes ist und $q_{E_1}$ und $q_{E_2}$ die Zustandssummen der (beiden) Edukte sind.
Manchmal ist auch die Aktivierungsenergie $E_a$ und der Energie-Unterschied zwischen Edukt und Produkt $\Delta E_{ab}$ gegeben, aber $E_b$ wird gesucht. Dann ist
$$ E_b = E_a - E_{ab} $$
Tipps für Aufgaben
Meist wird nur $k_{uni}$ betrachtet, da es sonst viel zu lange geht. Betrachte nochmal die Formel
$$ k_{uni} = \frac{1}{h \beta} \frac{q^{\ddagger}}{q_{E}} e^{-\beta E_a} $$
Für den Bruch musst du häufig nicht alle Zustandssummen einzeln berechnen, vieles kürzt sich weg. Genauer:
$$ \begin{aligned} &\text{Wenn } m^{\ddagger} = m_E \text{ dann } \frac{q_{trans}^{\ddagger}}{q_{trans, E}} = 1 \\ &\text{Wenn Wellenzahlen } \tilde{\nu}^{\ddagger} = \tilde{\nu}_{E} \text{ dann } \frac{q_{vib}^{\ddagger}}{q_{vib, E}} = 1 \\ &\text{Wenn Rotationskonstanten } B^{\ddagger} = B_E \text{ dann } \frac{q_{rot}^{\ddagger}}{q_{rot, E}} = 1 \end{aligned} $$
Ein häufiger Fehler passiert beim Berechnen des Exponents $-\beta E_a$ mit den Einheiten: $E_a$ kann sowohl in Joule, als auch in Joule/mol angegeben werden. Wenn du $E_a$ in Joule/mol hast, musst du es noch mit der Avogadro-Konstante $N_A$ multiplizieren, um auf Joule zu kommen, da $[\beta] = [\text{J}].$
Stosstheorie
In der Stosstheorie betrachten wir die Reaktion als Stoss zweier Moleküle. Die Geschwindigkeitskonstante ist dann gegeben durch
$$ k = \abk{\sigma} \abk{v_{rel}} $$
wobei $\abk{\sigma}$ der mittlere Reaktionsquerschnitt und $\abk{v_{rel}} = \sqrt{\frac{8 k_B T}{\pi \mu}}$ die mittlere relative Geschwindigkeit ist.
Modelle für Reaktionsquerschnitte
Der nicht-triviale Teil ist es, den Reaktionsquerschnitt $\sigma$ zu bestimmen. Dazu gibt es verschiedene Modelle, die wir uns jetzt anschauen.
Modell harter Kugeln
Im Modell harter Kugeln, betrachten wir die Reaktion als Stoss zweier Kugeln. Die Kugeln haben einen gewissen Radius $r$ und die Reaktion findet statt, wenn sich die Kugeln berühren. Dies gibt uns den Reaktionquerschnitt
$$ \sigma_0 = \pi (r_1 + r_2)^2 $$
der also unabhängig von der Energie der Reaktanden ist.
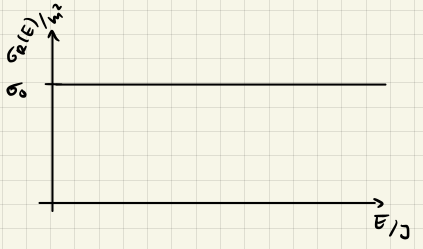
Damit gilt für die Geschwindigkeitskonstante
$$ k(T) = \sigma_0 v_{rel} = \pi (r_1 + r_2)^2 \sqrt{\frac{8 k_B T}{\pi \mu}} $$
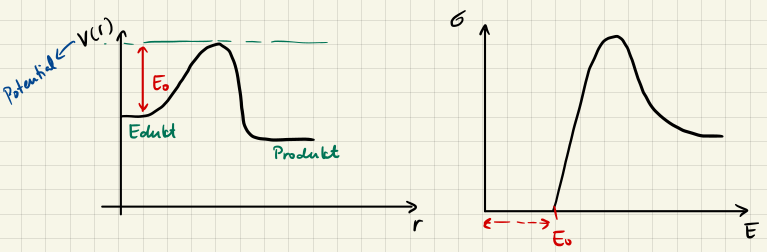
Modell harter Kugeln mit Schwellenenergie $E_0$
Etwas realistischer wird das Modell harter Kugeln, wenn wir eine Schwellenenergie $E_0$ einführen. Die Reaktion findet dann nur statt, wenn die Reaktanden eine Energie grösser als $E_0$ haben. Dies führt zu einem modifizierten Reaktionsquerschnitt
$$ \sigma = \sigma_0 \Theta(E-E_0) $$
wobei $\Theta(x) = \cases{0 & falls x < 0 \\ 1 & falls x > 0}$ die Heaviside-Funktion ist.
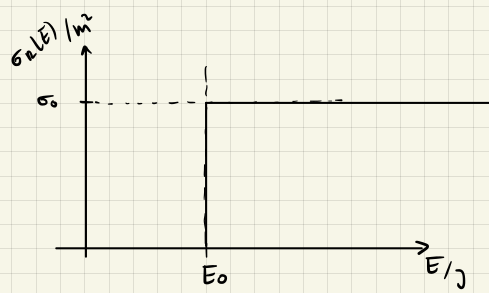
Der durchschnittliche Reaktionsquerschnitt ist dann gegeben durch
$$ \abk{\sigma} = \sigma_0 \left(1 + \beta E_0 \right) e^{-\beta E_0} $$
womit wir die Geschwindigkeitskonstante
$$ k(T) = \abk{\sigma} \abk{v_{rel}} = \sigma_0 \left(1 + \beta E_0 \right) e^{-\beta E_0} \sqrt{\frac{8 k_B T}{\pi \mu}} $$
erhalten.
Modell mit Schwellenenergie und langsam wachsendem $\sigma$
Das Modell mit Schwellenenergie ist noch nicht ganz realistisch, da der Reaktionsquerschnitt $\sigma$ nicht abrupt auf 0 fällt, sondern langsam abnimmt. Dies können wir mit einem exponentiellen Abfall modellieren
$$ \abk{\sigma} = \sigma_0 e^{-\beta E_0} $$
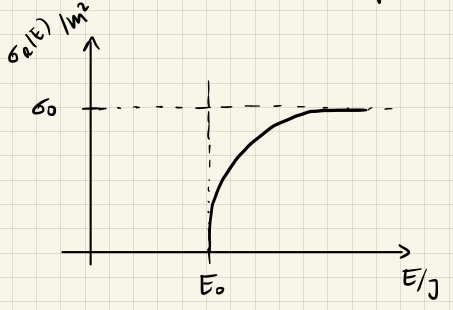
Womit die Geschwindigkeitskonstante durch
$$ k(T) = \abk{\sigma} \abk{v_{rel}} = \sigma_0 e^{-\beta E_0} \sqrt{\frac{8 k_B T}{\pi \mu}} $$
Arrhenius
Das Arrhenius-Gesetz versucht die Geschwindigkeitskonstante $k$ als Funktion der Temperatur $T$ zu beschreiben. Es ist gegeben durch
$$ k(T) = A e^{-\beta E_a} $$
oder in linearisierter Form
$$ \ln k(T) = \ln A - \beta E_a $$
Dabei ist $A$ eine reaktionsspezifische Konstante und $E_a$ die Aktivierungsenergie, definiert durch
$$ E_a = -R \dd{\ln k(T)}{\frac{1}{T}} = R T^2 \dd{\ln k(T)}{T} $$
Grafisch aufgetragen sieht das so aus:
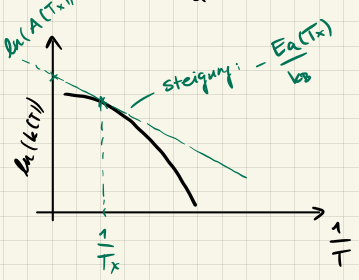
Oft nehmen wir an, dass $A$ und $E_a$ unabhängig von der Temperatur sind, was aber im Allgemeinen nicht stimmt (just to keep in mind).
Vergleichen wir das mit dem Modell harter Kugeln, so können wir den Faktor $A$ als eine Art Wahrscheinlichkeitsfaktor interpretieren, der bestimmt wann ein Zusammenstoss zu einer Reaktion führt
$$ \frac{k(\text{Arrhenius})}{k(\text{harte Kugeln})} = \text{"Jeder wievielte Stoss führt zu einer Reaktion"} $$
Linienverbreiterung
In den Naturwissenschaften betrachten wir oft Spektren, die idealerweise aus scharfen Linien bestehen. In der Realität sind die Linien aber oft verbreitert. Um diese Verbreiterung zu beschreiben betrachten wir die FWHM (Full Width at Half Maximum, $\Gamma$), also die Breite der Linie bei halber Höhe:
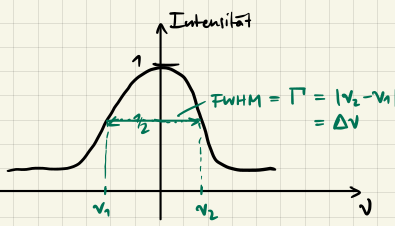
Dabei gibt es drei für uns relevante Arten von Linienverbreiterung:
Natürliche Linienbreite
Die natürliche Linienbreite müsste quantenmechanisch berechnet werden, wir nehmen hier einfach an, dass sie gegeben ist durch
$$ k_{eff} = 2 \pi \Gamma $$
Doppler-Verbreiterung
Die Doppler-Verbreiterung ergibt sich aus der thermischen Bewegung der Moleküle und ist gegeben durch
$$ \Delta \nu_D = \sqrt{8 \ln 2} \sqrt{\frac{k_B T}{m c^2}} \nu_0 $$
wobei $\nu_0$ die (zentrale) Frequenz der Linie ist.
Stossverbreiterung
Die Stossverbreiterung ergibt sich aus der Stosstheorie und ist gegeben durch
$$ k_{eff} = \sqrt{\frac{8 k_B T}{\pi \mu}} \abk{\sigma} [M] $$
Morgen 2 - Diffusion, Kettenreaktionen, Matrix & Enzymkinetik
Diffusion
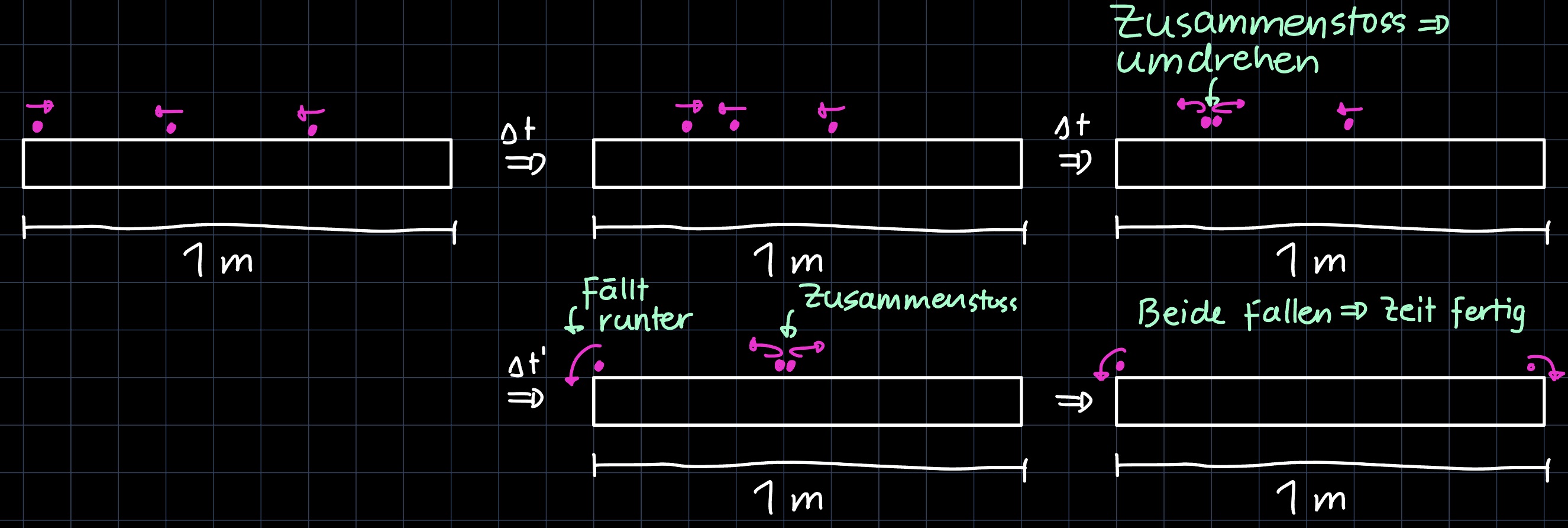
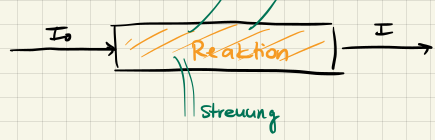
Diffusion ist der Prozess, bei dem sich Teilchen aufgrund ihrer thermischen Energie in einem Medium ausbreiten. Die Diffusion ist sehr wichtig für die Kinetik, da potentielle Reaktionspartner aufeinander treffen müssen um überhaupt eine Reaktion zu ermöglichen!
Betrachte eine Reaktion der Form
$$ \ce{A + B -> Produkte} $$
- Anfangsbedingungen: $A$ und $B$ sind Anfangs statistisch verteilt
- Anfangsphase: Die Reaktion soll schnell sein, d.h. benachbarte $\ce{A}$ und $\ce{B}$ Moleküle reagieren schnell ab. Dadurch entsteht ein Konzentrationsgradient.
- Stationäre Phase (Nichtgleichgewicht): Die Reaktion verläuft unter Aufrechterhaltung des Konzentrationsgradienten, indem $A/B$ durch Diffusion nachgeliefert werden.
Das ganze noch bildlich dargestellt:
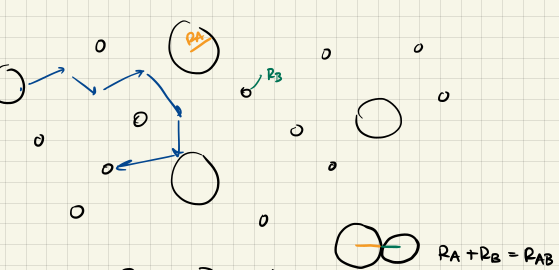
Gleichungen
Für die meisten Reaktionen kann der Konzentrationsgradient und somit der Einfluss der Diffusion vernachlässigt werden und wir haben unser altbekanntes Geschwindigkeitsgesetz
$$ v = k c_A \cdot c_B $$
Reagieren die Stoffe jedoch so schnell, dass der Konzentrationsgradient gross ist, so bestimmt die Diffusion, wie gross er in der stationären Phase ist und das Geschwindigkeitsgesetz muss zu
$$ v = k_{eff} c_A \cdot c_B $$
angepasst werden. Die effektive Geschwindigkeitskonstante $k_{eff}$ ist dabei gegeben durch
$$ k_{eff} = \frac{4 \pi R_{AB} D_{AB}}{1+ \frac{4 \pi R_{AB} D_{AB}}{k}} $$
wobei $R_{AB}$ der Reaktionsradius ist, d.h. der Radius, in dem sich die Reaktionspartner treffen müssen (meist $R_A+R_B$) und $D_{AB} = D_A + D_B$ die Diffusionskonstante, die gegeben werden muss. Wir erkennen hier, dass im Limit
$$ k \ll 4 \pi R_{AB} D_{AB} $$
die Geschwindigkeitskonstante $k_{eff}$ der Geschwindigkeitskonstante $k$ entspricht, was mit unserer Intuition übereinstimmt.
Im Limit der Diffusionskontrolle
$$ k \gg 4 \pi R_{AB} D_{AB} $$
hingegen erhalten wir
$$ k_{eff} = \frac{4 \pi R_{AB} D_{AB}}{1+ \frac{4 \pi R_{AB} D_{AB}}{k}} \approx 4 \pi R_{AB} D_{AB} $$
Grundsätzlich gilt
- Gase: Die Diffusionskontrolle ist bedeutungslos
- Flüssigkeiten: Bei schnellen Reaktionen häufig Diffusionskontrolle
Kettenreaktionen
Kettenreaktionen sind Reaktionen, bei denen ein Reaktionsprodukt wieder als Reaktionspartner auftritt. Deswegen sprechen wir auch von einer geschlossenen Folge. Einige wichtige Begriffe dazu sind:
- Kettenstart: Eine Reaktion, die die Kette startet
- Kettenträger: Eine Reaktion, die die Kette aufrecht erhält
- Kettenabbruch: Eine Reaktion, die die Kette beendet
- Inhibierung/Hemmung: Eine Reaktion, die die Kette verlangsamt
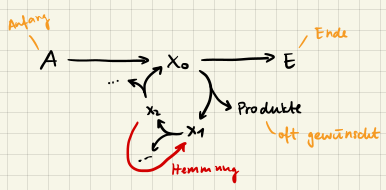
Ein Beispiel dazu ist die (radikale) Bromwasserstoffbildung
$$ \begin{aligned} \ce{Br2 + H2 &->[M] 2 Br^{\ast}} \qquad &\text{Kettenstart} \\ \ce{Br^{\ast} + H2 &-> HBr + H^{\ast}} \qquad &\text{Kettenträger} \\ \ce{H^{\ast} + HBr &-> H2 + Br^{\ast}} \qquad &\text{Hemmung} \\ \ce{H^{\ast} + Br2 &-> HBr + Br^{\ast}} \qquad &\text{Kettenträger} \\ \ce{2 Br^{\ast} &->[M] Br2} \qquad &\text{Kettenabbruch} \\ \ce{2 H^{\ast} &->[M] H2} \qquad &\text{Kettenabbruch} \\ \ce{Br^{\ast} + H^{\ast} &->[M] HBr} \qquad &\text{Kettenabbruch} \end{aligned} $$
Stabilitätsanalyse
Betrachten wir eine (verzweigte) Kettenreaktion der Form
$$ \begin{aligned} (1) \qquad & I_1 \rightarrow I^{\ast} \\ (2) \qquad & I^{\ast} + R \xrightarrow{k_p} P + I^{\ast} \\ (3) \qquad & I^{\ast} \xrightarrow{k_v} \alpha I^{\ast} \qquad (\text{Verzweigung}) \\ (4) \qquad & I^{\ast} \xrightarrow{k_a} I_1 \qquad (\text{Abbruch}) \end{aligned} $$
so erhalten wir für $[I^{\ast}]$ das Geschwindigkeitsgesetz
$$ \begin{aligned} \dd{[I^{\ast}]}{t} &= v_1 + k_v (\alpha - 1) [I^{\ast}] - k_a [I^{\ast}] \\ &= v_1 + (k_v (\alpha - 1) - k_a)[I^{\ast}] \\ \end{aligned} $$
wobei $v_1$ die Geschwindigkeit der Reaktion $(1)$ ist. Nehmen wir an, $v_1$ sei konstant, so erhalten wir nach Definition von $\phi = k_a - k_v (\alpha - 1)$
$$ [I^{\ast}] (t) = \frac{v_1}{\phi} \left( e^{\phi t} - 1 \right) $$
Aus der Reaktion $(2)$ erhalten wir für die Geschwindigkeit der Produktbildung
$$ \begin{aligned} \dd{[P]}{t} &= k_p [I^{\ast}] [R] = \frac{k_p v_1}{\phi} \left( e^{\phi t} - 1 \right) [R] \\ &\approx k_p' [I^{\ast}] [R] = \frac{k_p v_1}{\phi} \left( e^{\phi t} - 1 \right) \end{aligned} $$
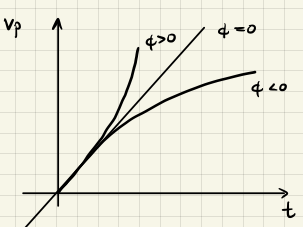
wobei wir im letzten Schritt die Annahme getroffen haben, dass $[R]$ konstant ist, da $[R] \gg [I^{\ast}].$ Untersuchen wir die drei Fälle $\phi > 0$, $\phi = 0$ und $\phi < 0,$ so erkennen wir
- $\phi < 0$: Die Konzentration $[I^{\ast}]$ ist nach einiger Zeit konstant $\rightarrow$ Quasistationär, d.h. stabil
- $\phi = 0$: Die Konzentration $[I^{\ast}]$ wächst linear an, d.h. instabil
- $\phi > 0$: Die Konzentration $[I^{\ast}]$ wächst exponentiell an, d.h. instabil
Kinetische Matrix
Die kinetische Matrix ist eine Methode, um die Geschwindigkeitsgesetze von komplexeren Reaktionen erster Ordnung zu bestimmen. Der Formalismus betrachtet dabei Reaktionen der Form
$$ A_L \xrightarrow{-K_{ML}} A_M $$
wobei $A_L$ und $A_M$ die Edukte und Produkte der Reaktion sind und $-K_{ML}$ die Geschwindigkeitskonstante. Setzen wir dann $N$ Reaktionen erster Ordnung zusammen, so erhalten wir das System
$$ \begin{aligned} -\dd{c_1}{t} &= K_{11} c_1 + K_{12} c_2 + \dots + K_{1N} c_N\\ \vdots & \\ -\dd{c_N}{t} &= K_{N1} c_1 + K_{N2} c_2 + \dots + K_{NN} c_N \end{aligned} $$
Diese gekoppelten Differentialgleichungen einzeln zu lösen wäre sehr mühsam, aber glücklicherweise gibt uns die Matrix-Form
$$ -\dd{\vec{c}}{t} = K \vec{c}(t) $$
direkt die Lösung als
$$ \vec{c}(t) = \exp(-Kt) \vec{c}_0 $$
Wie rechnen wir das nun aber aus? Betrachten wir dazu ein einfaches Beispiel
$$ A_1 \xrightleftharpoons[k_b]{k_a} A_2 $$
mit den Geschwindigkeitskonstanten $k_a = 2, k_b = 0.$ Gehe in folgenden Schritten vor
\1. Schreibe die Geschwindigkeitskonstanten anhand des Formalismus auf
$$ \begin{aligned} &A_1 \xrightleftharpoons[-K_{12}]{-K_{21}} A_2 \\ &\Rightarrow - K_{12} = k_b = 0 \qquad - K_{21} = k_a = 2 \end{aligned} $$
\2. Stelle die kinetische Matrix auf. Dabei bezeichnen die Indizes von $K_{ij}$ die Zeile $i$ und Spalte $j$. Für die noch unbekannten Diagonal-Elemente gilt $K_{jj} = - \sum_{i \neq j} K_{ij}$
$$ \begin{pmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{pmatrix} = \begin{pmatrix} -K_{21} & K_{12} \\ K_{21} & -K_{12} \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ -2 & 0 \end{pmatrix} $$
\3. Nun haben wir die kinetische Matrix. Wir sind aber noch nicht fertig, da wir noch das Exponential $\exp(-Kt)$ ausrechnen rechnen müssen. Das geht am besten, indem wir die Matrix diagonalisieren. Dazu berechnen wir zuerst die Eigenwerte $\lambda$ und Eigenvektoren $\vec{v}$ der Matrix $K$.
$$ \begin{aligned} &\det(K - \lambda \mathbb{1}) = 0 \\ &\Rightarrow \det \begin{pmatrix} 2 - \lambda & 0 \\ -2 & -\lambda \end{pmatrix} = 0 \\ &\Rightarrow (2 - \lambda) (-\lambda) - (-2) \cdot 0 = 0 \\ &\Rightarrow \lambda_1 = 0, \lambda_2 = 2 \end{aligned} $$
\4. Nun berechnen wir die Eigenvektoren $\vec{v}_{1,2}$ zu den Eigenwerten $\lambda_{1,2}$.
$$ \begin{aligned} \begin{pmatrix} 2 & 0 \\ -2 & 0 \end{pmatrix} \begin{pmatrix} v_{1,1} \\ v_{1,2} \end{pmatrix} &= 0 \qquad \Rightarrow v_{11} = 0, v_{1,2} = 1 \qquad \Rightarrow \vec{v}_1 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{aligned} $$
$$ \begin{aligned} \begin{pmatrix} 2 & 0 \\ -2 & 0 \end{pmatrix} \begin{pmatrix} v_{2,1} \\ v_{2,2} \end{pmatrix} &= 2 \begin{pmatrix} v_{2,1} \\ v_{2,2} \end{pmatrix} \qquad \Rightarrow v_{2,1} = 1, v_{2,2} = -1 \qquad \Rightarrow \vec{v}_2 = \begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{aligned} $$
\5. Nun können wir das Exponential einfach ausrechnen
$$ \exp(-Kt) = \begin{pmatrix} \vec{v}_1 & \vec{v}_2 \end{pmatrix} \begin{pmatrix} e^{-\lambda_1 t} & 0 \\ 0 & e^{-\lambda_2 t} \end{pmatrix} \begin{pmatrix} \vec{v}_1 & \vec{v}_2 \end{pmatrix}^{-1} = \begin{pmatrix} 0 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & e^{-2t} \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} e^{-2t} & 0 \\ 1- e^{-2t} & 1 \end{pmatrix} $$
\6. Die Lösung der Differentialgleichung ist also
$$ \vec{c}(t) = \exp(-Kt) \vec{c}_0 = \begin{pmatrix} e^{-2t} & 0 \\ 1- e^{-2t} & 1 \end{pmatrix} \begin{pmatrix} c_1(0) \\ c_2(0) \end{pmatrix} = \begin{pmatrix} c_1(0) e^{-2t} \\ c_1(0) (1 - e^{-2t}) + c_2(0) \end{pmatrix} $$
Enzymkinetik
Betrachte die typische Michaelis-Menten Reaktion
$$ E + S \xrightleftharpoons[k_{-1}]{k_1} ES \xrightarrow{k_2} E + P $$
wobei $E$ das Enzym, $S$ das Substrat, $ES$ das Enzym-Substrat-Komplex und $P$ das Produkt ist. Uns interessiert die Produktbildungsgeschwindigkeit
$$ v = \dd{[P]}{t} = k_2 [ES] $$
die wir in Abhängigkeit der Substrat-Konzentration $[S]$ ausdrücken möchten. Dazu nehmen wir Quasi-Stationärität (QS) für $[ES]$ an, d.h. $[ES]$ ist konstant und schreiben das Geschwindigkeitsgesetz auf
$$ \dd{[ES]}{t} = k_1 [E] [S] - k_{-1} [ES] - k_2 [ES] = 0 $$
woraus wir $[ES]$ ausdrücken können durch
$$ [ES] = \frac{k_1}{k_{-1} + k_2} [E] [S] $$
Benutzen wir nun die Massenerhaltung für $[E]$, d.h. $[E]_0 = [E] + [ES]$, so erhalten wir
$$ [ES] = \frac{k_1}{k_{-1} + k_2} \left( [E]_0 - [ES] \right) [S] $$
was sich nach $[ES]$ auflösen lässt zu
$$ [ES] = \frac{\frac{k_1}{k_{-1} + k_2} [E]_0 [S]}{1 + \frac{k_1}{k_{-1} + k_2} [S]} = \frac{[E]_0 [S]}{K_M + [S]} $$
wobei wir die Michaelis-Konstante $K_M = \frac{k_{-1} + k_2}{k_1}$ definiert haben. Setzen wir nun $[ES]$ in die Produktbildungsgeschwindigkeit ein, so erhalten wir
$$ v = k_2 \frac{[E]_0 [S]}{K_M + [S]} $$
Plots und Linearisierungen
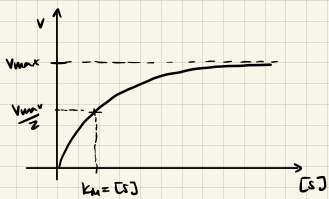
Betrachte die Limits
- $[S] \ll K_M$: $v \approx \frac{k_2 [E]_0 [S]}{K_M} \rightarrow$ Reaktion ist substratlimitiert
- $[S] = K_M$: $v = \frac{k_2 [E]_0}{2} = \frac{v_{max}}{2} \rightarrow$ Reaktion ist halbsättigend
- $[S] \gg K_M$: $v \approx \frac{k_2 [E]_0 [S]}{[S]} = k_2 [E]_0 \rightarrow$ Reaktion ist enzymlimitiert
Definieren wir $v_{max} = k_2 [E]_0,$ so können wir die Abhängigkeit der Produktbildungsgeschwindigkeit von der Substrat-Konzentration darstellen als
Da die Steigung hier nicht konstant ist, ist es jedoch schwierig die vorkommenden Parameter zu bestimmen. Um das zu vereinfachen haben wir im Unterricht drei Linearisierungen kennengelernt.
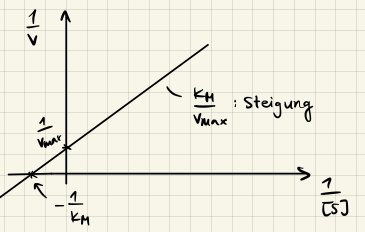
Lineweaver-Burk
$$ \frac{1}{v} = \frac{K_M}{v_{max}} \frac{1}{[S]} + \frac{1}{v_{max}} $$
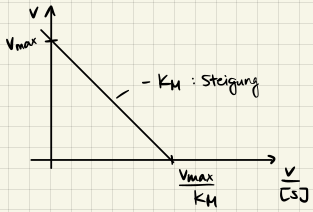
Eadie-Hofstee
$$ v = -\frac{v_{max}}{K_M} [S] + v_{max} $$
Dixon Hanes
$$ \frac{[S]}{v} = \frac{K_M}{v_{max}} + \frac{1}{v_{max}}[S] $$
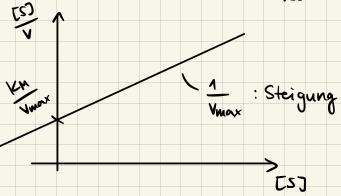
Kompetitive Hemmung
Bei der kompetitiven Hemmung bildet ein Inhibitor $I$ einen Komplex $EI$ mit dem Enzym $E$, der nicht mehr in der Lage ist, das Substrat $S$ zu binden. Wir betrachten also nun die zwei Reaktionen
$$ \begin{aligned} E + S &\xrightleftharpoons[k_{-1}]{k_1} ES \xrightarrow{k_2} E + P \\ E + I &\xrightleftharpoons[k_{-3}]{k_3} EI \end{aligned} $$
Auch hier möchten wir die Produktbildungsgeschwindigkeit bestimmen
$$ v = \dd{[P]}{t} = k_2 [ES] $$
Nehmen wir wiederum QS für $[ES]$, sowie für $[EI]$ an, so gilt
$$ \begin{aligned} \dd{[ES]}{t} &= k_1 [E] [S] - k_{-1} [ES] - k_2 [ES] &= 0 \\ \dd{[EI]}{t} &= k_3 [E] [I] - k_{-3} [EI] &= 0 \end{aligned} $$
sowie die Massenerhaltung für $[E]$
$$ [E]_0 = [E] + [ES] + [EI] $$
Umformen und auflösen ergibt
$$ [E] = \frac{[E]_0}{1 + \frac{1}{K_M} [S] + \frac{1}{K_I} [I]} $$
wobei wir die Michaelis-Konstante $K_M = \frac{k_{-1} + k_2}{k_1}$ und analog die Inhibitions-Konstante $K_I = \frac{k_{-3}}{k_3}$ definiert haben. Setzen wir nun $[E]$ in die Produktbildungsgeschwindigkeit ein, so erhalten wir
$$ \begin{aligned} v &= k_2 \frac{[E]_0 [S]}{K_M + \frac{K_M}{K_I} [I] + [S]} \\ &= \frac{v_{max} [S]}{K_M' + [S]} \end{aligned} $$
mit $K_M' = K_M \left( 1 + \frac{[I]}{K_I} \right)$ und $v_{max} = k_2 [E]_0.$ Den Parameter $1 + \frac{[I]}{K_I}$ nennen wir den Hemmungsfaktor $\alpha$ und wir können ihn einfach aus dem Lineweaver-Burk Plot ablesen:
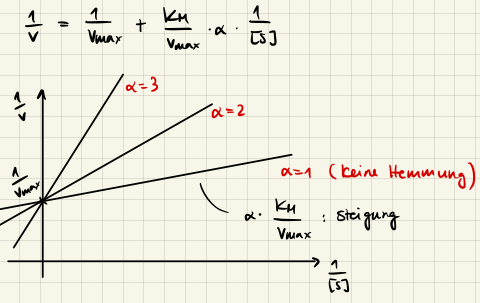
Unkompetitive Hemmung
Bei der unkompetitiven Hemmung bildet ein Inhibitor $I$ einen Komplex $ESI$ mit dem Enzym-Substrat-Komplex $ES$, der nicht mehr in der Lage ist, direkt das Produkt $P$ zu bilden. Wir betrachten also nun die zwei Reaktionen
$$ \begin{aligned} E + S &\xrightleftharpoons[k_{-1}]{k_1} ES \xrightarrow{k_2} E + P \\ E + I &\xrightleftharpoons[k_{-3}]{k_3} ESI \end{aligned} $$
Nach einer analogen Vorgehensweise wie bei der kompetitiven Hemmung erhalten wir die Produktbildungsgeschwindigkeit
$$ v = \frac{v_{max}' [S]}{K_M' + [S]} $$
mit $K_M' = \frac{K_M}{\alpha'}$ und $v_{max}' = \frac{k_2 [E]_0}{\alpha'}.$ Die Linearisierung durch Lineweaver-Burk gibt uns wieder den Hemmungsfaktor $\alpha' = 1 + \frac{[I]}{K_I}.$
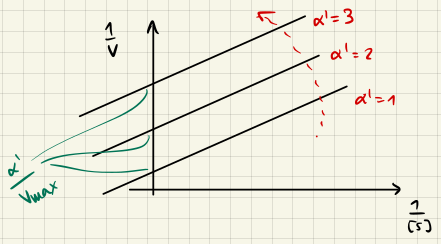
Nichtkompetitive Hemmung
Die nichtkompetitive Hemmung ist eine Mischform der kompetitiven und unkompetitiven Hemmung. Wir betrachten also nun die drei Reaktionen
$$ \begin{aligned} E + S &\xrightleftharpoons[k_{-1}]{k_1} ES \xrightarrow{k_2} E + P \\ E + I &\xrightleftharpoons[k_{-3}]{k_3} EI \\ ES + I &\xrightleftharpoons[k_{-4}]{k_4} ESI \end{aligned} $$
und erhalten durch viel rechnen die Produktbildungsgeschwindigkeit
$$ v = \frac{v_{max} [S]}{\alpha K_H + \alpha' [S]} $$
Die Linearisierung für $\alpha = \alpha'$ gibt uns dann
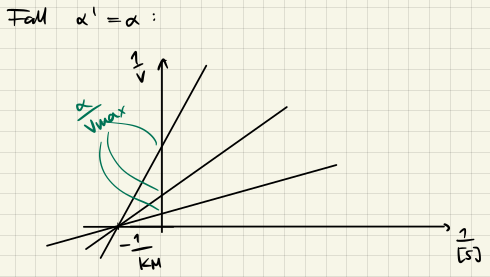
Nachmittag 2 - Stossmodelle Experimentelle & Mathematische Methoden
Absorptionsspektroskopie
Lambert-Beer
Das Lambert-Beer Gesetz beschreibt die Abschwächung der Intensität eines Lichtstrahls beim Durchgang durch ein Medium:
$$ \begin{aligned} dI &= \sigma \cdot I \cdot c \cdot dx \\ \ln \left( \frac{I_0}{I} \right) &= \sigma \cdot c \cdot l \end{aligned} $$
wobei $I_0$ die Intensität des einfallenden Lichts, $I$ die Intensität des austretenden Lichts, $\sigma$ der Absorptionskoeffizient, $c$ die Konzentration des Absorbers und $l$ die Länge des zurückgelegten Pfades ist. $\sigma$ bezeichnet den Wirkungsquerschnitt und ist eine materialspezifische Konstante.
Verbindung Reaktionsquerschnitt $\sigma_R$
Betrachten wir nochmal das Lambert-Beer Gesetz:
$$ \ln\left(\frac{I_0}{I}\right) = \sigma \cdot c \cdot l $$
dann ist $\sigma$ nicht $\sigma_R,$ sondern eine Kombination aus $\sigma_R$ und dem Stossquerschnitt $\sigma_S:$
$$ \sigma = \sigma_R + \sigma_S $$
Kinetik geladener Teilchen
Betrachte eine Reaktion der Form
$$ \ce{A^{$Z_A4} + B^{$Z_B$} -> Produkte} $$
mit den Ladungen $Z_A$ und $Z_B.$ Da es hier eine elektrostatische Wechselwirkung zwischen den Reaktionspartnern gibt, haben wir eine neue Formel für die Reaktionsgeschwindigkeit
$$ v_c = \frac{1}{h \beta} \frac{\gamma_A \gamma_B}{\gamma^{\ddagger}} \cdot e^{\frac{-\Delta^{\ddagger} G}{RT}} \cdot (c^{\ast})^{-1} \cdot [\ce{A}^{Z_A}] \cdot [\ce{B}^{Z_B}] $$
mit den Aktivitätskoeffizienten $\gamma_i$ und $(c^{\ast})^{-1} = \frac{1}{V^{\ast}}$ damit die Einheiten aufgehen (Einheitskonzentration). Betrachten wir die Geschwindigkeitskonstante
$$ k_c = \frac{1}{h \beta} \frac{\gamma_A \gamma_B}{\gamma^{\ddagger}} \cdot e^{\frac{-\Delta^{\ddagger} G}{RT}} \cdot (c^{\ast})^{-1} $$
so können wir diese nach Anwendung des Logarithmus aufteilen in die Summanden
$$ \begin{aligned} \ln(k_c) &= \ln(k') + \ln \left( \frac{\gamma_A \gamma_B}{\gamma^{\ddagger}} \right) \\ \text{mit} \quad k' &= \frac{1}{h \beta} \cdot e^{\frac{-\Delta^{\ddagger} G}{RT}} \cdot (c^{\ast})^{-1} \end{aligned} $$
Debye-Hückel für kleine Ionenstärken
Um die Aktivitätskoeffizienten zu berechnen, benutzen wir die Debye-Hückel Näherung für kleine Ionenstärken ($I \lt 0.1 \, \mathrm{mol/kg}$)
$$ \log_{10} \gamma_i = -\beta \cdot Z_i^2 \cdot \sqrt{I} $$
mit der Ionenstärke $I = \frac{1}{2} \sum_i c_i \cdot Z_i^2$ und $\beta$ einer gegebenen Konstante. Setzen wir dies in das obige Geschwindigkeitsgesetz ein, so erhalten wir die Brönsted-Gleichung
$$ \log_{10} k_c = \log_{10} k' + 2 \beta Z_A Z_B \sqrt{I} $$
Debye-Hückel für nicht-kleine Ionenstärken
Für grössere Ionenstärken müssen wir die Debye-Hückel Näherung anpassen. Wir erhalten
$$ -\ln \gamma_i = \alpha Z_i^2 \cdot \sqrt{I} \left( 1 + 2 \alpha \sqrt{I} \frac{a}{\rho} \right)^{-1} $$
wobei $\rho = \frac{e_0^2}{4 \pi \varepsilon \varepsilon_0 k_B T}, \alpha = \sqrt{2\pi N_A \rho_L \rho^3}, e_0$ die Elementarladung, $\rho_L$ die Dichte des Lösungsmittels und $a$ der Ionendurchmesser ist. Solche Sachen denke ich werden aber wenn überhaupt gefragt nochmal erklärt.
Experimentelle Methoden
Absorptionsspektroskopie
Wir benutzen das Lambert-Beer Gesetz
$$ A = \log \left( \frac{I_0}{I} \right) = \sigma (\nu) \cdot c \cdot l $$
was sich umformen lässt zu
$$ c(t) = \frac{A(t)}{\sigma (\nu) \cdot l} $$
Was wir messen ist die Absorption $A(t)$ in Abhängigkeit der Frequenz $\nu.$ Ein Spektrum ist eine Auftragung von $A(\nu)$ gegen $\nu.$
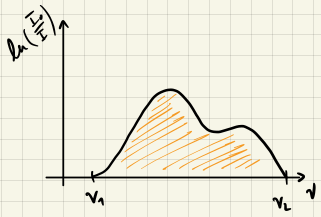
Fall 1: Produkt- und Edukt-Spektren überlappen nicht
Absorbieren die Edukte und Produkte bei unterschiedlichen Wellenlängen, so können fällt es besonders leicht, die Konzentrationen der Edukte und Produkte zu bestimmen.
$$ c_{Edukt}(t) = \frac{A_{Edukt}(t)}{\sigma_{Edukt} (\nu) \cdot l} $$
$$ c_{Produkt}(t) = \frac{A_{Produkt}(t)}{\sigma_{Produkt} (\nu) \cdot l} $$
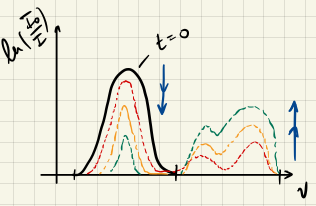
Fall 2: Produkt- und Edukt-Spektren überlappen
Absorbieren die Edukte und Produkte bei den ähnlichen Wellenlängen, können wir die Konzentrationen nicht mehr einfach so ablesen, da die Absorption durch die Formel
$$ A(t) = \ln \left( \frac{I_0}{I} \right) = \left( \sigma_{Edukt} (\nu) \cdot c_{Edukt} + \sigma_{Produkt} (\nu) \cdot c_{Produkt} \right) \cdot l $$
beschrieben wird. Das Spektrum sieht dann etwa so aus
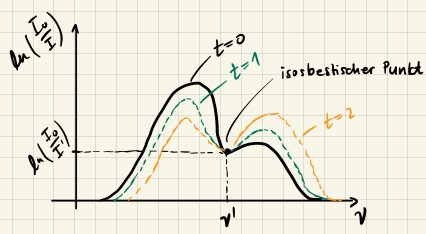
Isosbestischer Punkt
Falls es im Spektrum einen Punkt gibt, wo sich die Absorbanz zeitlich nicht verändert, so deutet dies auf eine einfache Stöchiometrie hin. Für eine Gleichgewichtsreaktion zwischen zwei Stoffen beispielsweise
$$ \begin{aligned} l \cdot \sum_i \sigma_i c_i &= \text{konstant} \\ \Rightarrow -\nu_1 \sigma_1 &= \nu_2 \sigma_2 \end{aligned} $$
Halbwertszeitmethode
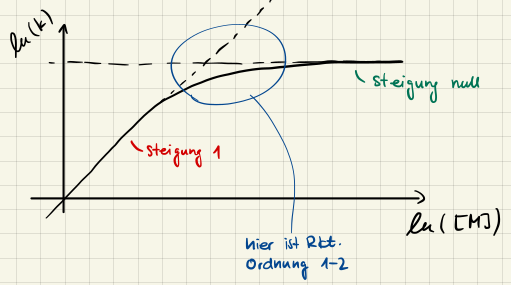
Trage die Halbwertszeit $t_{1/2}$ gegen die Anfangskonzentration $c_0$ auf. Da dies dem Gesetz
$$ t_{1/2}(c_0) = \frac{2^{m-1}-1}{k(m-1)} \cdot c_0^{1-m} $$
Durch Anwendung des Logarithmus erhalten wir die Lineare Form
$$ \ln(t_{1/2}) = \ln \left( \frac{2^{m-1}-1}{k(m-1)} \right) + (1-m) \cdot \ln(c_0) $$
und durch lineare Regression können wir über die Steigung die Reaktionsordnung $m$ bestimmen.
Isolationsmethode
Nehmen wir alle Reaktanden ausser einem im Überschuss, so können wir die Konzentrationen dieser Reaktanden als konstant annehmen. Wir erhalten also das einfachere Geschwindigkeitsgesetz
$$ v_c = k_{eff} c^m $$
Durch Anwendung des Logarithmus erhalten wir die Lineare Form
$$ \ln(v_c) = \ln(k_{eff}) + m \cdot \ln(c) $$
und durch lineare Regression können wir über die Steigung die Reaktionsordnung $m$ bestimmen.
Methode der Anfangsgeschwindigkeiten
Betrachte das Geschwindigkeitsgesetz
$$ v_c = \frac{1}{\nu_1} \dd{c_1}{t} = k c_1^{m_1} \cdots $$
Am Anfang der Reaktion gilt
$$ v_c^0 \approx \frac{1}{\nu_1} \frac{\Delta c_1}{\Delta t} = k_{eff} c_1^{m_1} $$
wobei $v_c^0$ die Anfangsgeschwindigkeit ist. Durch Anwendung des Logarithmus erhalten wir die Lineare Form
$$ \ln(v_c^0) = \ln(k_{eff}) + m_1 \cdot \ln(c_1) $$
und durch lineare Regression können wir über die Steigung die Reaktionsordnung $m_1$ bestimmen.
Methode der Differentialquotienten
Diese Methode hilft uns Annäherungsweise die Geschwindigkeitskonstante $k$ zu bestimmen. Wir betrachten
$$ - \frac{\Delta c}{\Delta t} = k \abk{c}^m $$
mit $\abk{c} = \frac{c_1+c_2}{2}.$ Nach Anwendung des Logarithmus
$$ \ln \left( - \frac{\Delta c}{\Delta t} \right) = \ln(k) + m \cdot \ln(\abk{c}) $$
Mit der Annäherung für kleine $\Delta t$
$$ \dd{c}{t} \approx \frac{\Delta c}{\Delta t} = -k \abk{c}^m $$
erhalten wir die Geschwindigkeitskonstante
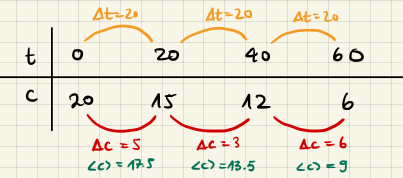
$$ k \approx -\frac{1}{\abk{c}^m} \cdot \frac{\Delta c}{\Delta t} $$
Die Idee sieht also in etwa so aus
Periodische Störung
Betrachten wir ein Gleichgewicht, welches periodisch, z.B. durch Ultraschall oder Druckwellen, gestört wird. Je nach Verhältnis der Störungsfrequenz $\omega$ und der Relaxationszeit $\tau_R = \frac{1}{k_{eff}}$ des Systems unterscheiden wir drei Fälle:
Fall 1: $\omega \tau_R \ll 1$
Die Probe relaxiert schnell. Damit ist die Auslenkung aus dem Gleichgewicht synchron mit der Störung.
Fall 2: $\omega \tau_R \approx 1$
Das System relaxiert langsam verglichen mit der Welle, jedoch schnell genug um der Welle zu folgen. Wir erhalten eine Phasenverschiebung $\phi(\omega) = \arctan(\omega\tau_R)$
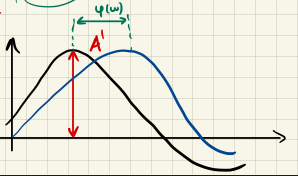
Für eine Anregung der Form $A \cdot \sin(\omega t)$ folgt die Auslenkung des Systems $\Delta(t) = c(t) - c_{eq}$ dem Verlauf
$$ \Delta(t) = \frac{A}{\sqrt{1+(\omega\tau_R)^2}} \cdot \sin(\omega t - \phi(\omega)) $$
Fall 3: $\omega \tau_R \gg 1$s
Die Reaktion ist sehr langsam und es kommt kaum zu einer Auslenkung aus dem Gleichgewicht.
Morgen 3 - Lindemann & Langevin
Lindemann-Mechanismus (Druckabhängigkeit von $k$)
Bei unimolekularen Reaktionen
$$ \ce{X_Z -> Produkte} $$
hatten wir gesagt, dass es eine Anregung durch einen Stosspartner $\ce{M}$ braucht. Dies kann genauer durch den Lindemann-Mechanismus beschrieben werden
$$ \begin{aligned} \ce{X_Z + M &->[$k_1$] X^{\ast} + M} \qquad & \text{Aktivierung} \\ \ce{X^{\ast} + M &->[$k_2$] X_Z + M} \qquad & \text{Desaktivierung} \\ \ce{X^{\ast} &->[$k_3$] Produkte} \qquad & \text{Reaktion} \end{aligned} $$
wobei $\ce{X^{\ast}}$ ein angeregter Zustand von $\ce{X_Z}$ ist. Der Energetische Verlauf ist in der folgenden Abbildung dargestellt
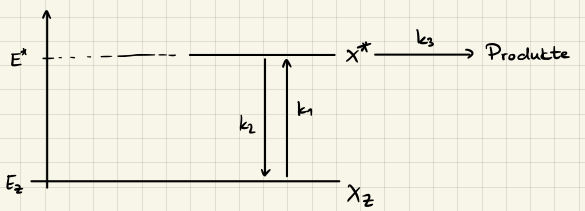
Um das Geschwindigkeitsgesetz aufzustellen können wir einfacher die zusammengefasste Reaktionsgleichung
$$ \ce{X_Z + M <=>[$k_a$][$k_d$] X^{\ast} + M ->[$k_r$] P + M} $$
verwenden. Mit Quasistationaritätsannahme für $\ce{X^{\ast}}$ erhalten wir
$$ \begin{aligned} \frac{\mathrm{d}[\ce{X^{\ast}}]}{\mathrm{d}t} &= k_a[\ce{X_Z}][\ce{M}] - k_d[\ce{X^{\ast}}][\ce{M}] - k_r[\ce{X^{\ast}}] = 0 \\ \Rightarrow [\ce{X^{\ast}}] &= \frac{k_a[\ce{X_Z}][\ce{M}]}{k_d[\ce{M}] + k_r} \end{aligned} $$
und damit das Geschwindigkeitsgesetz
$$ v = k_r[\ce{X^{\ast}}] = \frac{k_a k_r}{k_d + \frac{k_r}{[\ce{M}]}}[\ce{X_Z}][\ce{M}] = k_{eff} [\ce{X_Z}] $$
mit der effektiven Geschwindigkeitskonstante
$$ k_{eff} = \frac{k_a k_r}{k_d + \frac{k_r}{[\ce{M}]}} $$
Diese Gleichung lässt sich durch Kehrwertbildung leicht linearisieren
$$ \frac{1}{k_{eff}} = \frac{k_d}{k_r \cdot k_a} + \frac{1}{k_a} \cdot \frac{1}{[\ce{M}]} $$
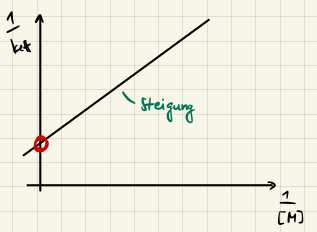
Niederdruckbereich
Im Niederdruckbereich ist $[\ce{M}]$ klein und damit ist der zweite Term $\frac{1}{k_a} \cdot \frac{1}{[\ce{M}]}$ dominant. Wir erhalten
$$ k_{eff} \approx k_a [\ce{M}] $$
Die Aktivierung ist also geschwindigkeitsbestimmend und die Reaktion ist 2. Ordnung.
Hochdruckbereich
Im Hochdruckbereich ist $[\ce{M}]$ gross und damit ist der erste Term $frac{k_d}{k_r \cdot k_a}$ dominant. Wir erhalten
$$ k_{eff} \approx \frac{k_d}{k_r \cdot k_a} $$
Die Reaktion ist also 1. Ordnung (0. Ordnung in $[\ce{M}]$) und der Reaktionsschritt ist geschwindigkeitsbestimmend.
Übergangsbereich
Den Übergangsbereich zwischen den zwei Bereichen können wir qualitativ durch die folgende Abbildung beschreiben
Langevin-Modell
Für Reaktionen von einem ungeladenen Molekül mit einem geladenen Molekül (Molekül-Ion-Reaktionen) können wir das Langevin-Modell verwenden. Moleküle und Ionen reagieren nicht gleich wie Moleküle untereinander, da durch die Polarisierbarkeit $\alpha$ der Moleküle eine Coulomb-Anziehung zwischen den Ladungen entsteht. Wir erhalten die Geschwindigkeitskonstante
$$ k = \sigma(E_t) \sqrt{\frac{2 E_t}{\mu}} = \sqrt{\frac{2 a} {\mu}} $$
mit $\sigma(E_t) = \sqrt{\frac{a}{E_t}}$ als Stossquerschnitt und $a = \frac{\alpha \cdot e^2}{8 \varepsilon_0^2}.$ Was wir hier erkennen können ist, dass die Geschwindigkeitskonstante in diesem Modell nicht mehr von der Energie abhängt!
Potentialfunktionen und zugehörige $\sigma_R(E)$
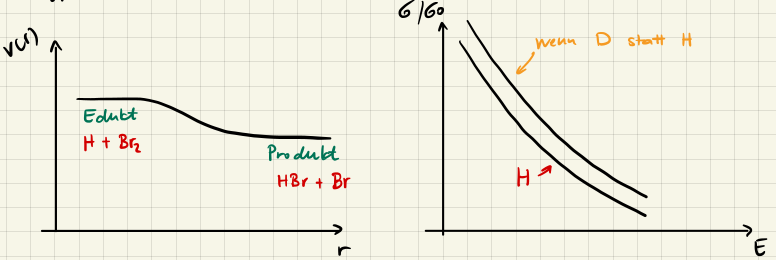
Typ I (normal)
Damit die Reaktion ablaufen kann muss die Aktivierungsenergie $E_0$ überwunden werden, also ist der Reaktionsquerschnitt $\sigma_R(E) = 0$ für $E < E_0.$ Für $E \gg E_0$ wird $\sigma_R(E)$ wieder abnehmen, da die Teilchen zu schnell sind um zu reagieren.
Typ II
Da keine Aktivierungsenergie benötigt wird, nimmt $\sigma_R(E)$ ab, wenn $E$ wächst, da die Teilchen zu schnell sind um zu reagieren.
Typ III
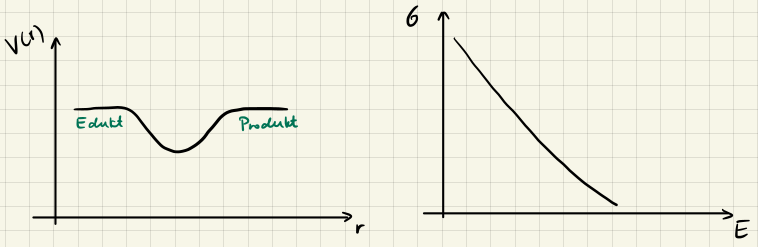
Auch hier wird keine Aktivierungsenergie benötigt, womit der Reaktionsquerschnitt $\sigma_R(E)$ abnimmt, wenn $E$ wächst.
Nachmittag 3 - Reserve & Repetition
Repetition der wichtigsten/schwierigsten Konzepte
Wir machen nochmal eine kurze Repetition der Teile, die am meisten Probleme bereitet haben/das tiefste Rating auf dem Understandometer erhalten haben aber trotzdem Prüfungsrelevant sind.
Quasistationarität
Betrachten wir ein komplexes Reaktionsnetzwerk, so möchten wir meist die Produktbildungsgeschwindigkeit in Abhängigkeit der Eduktkonzentration bestimmen. Da die Konzentrationen der Zwischenprodukte unbekannt sind, müssen wir Vereinfachungen treffen, um diese zu eliminieren. Eine wichtige solche Vereinfachung ist die Quasistationarität. Dabei nehmen wir an, dass die Konzentrationen der Zwischenprodukte sich sehr schnell einstellen, sodass wir die zeitliche Änderung der Konzentrationen vernachlässigen können. Einsetzen der Geschwindigkeitsgesetze führt dann zu einem System von Gleichungen, welches wir lösen können.
Grundsätzlich können wir für jegliche Radikale annehmen, dass die Konzentrationen quasistationär sind. Denn diese reagieren viel schneller ab, als sie gebildet werden. Da die Reaktionsgeschwindigkeit der Abbaureaktion von der Konzentration des Radikales abhängt, wird sich so schnell die Gleichgewichtskonzentration einstellen.
Vorgelagertes Gleichgewicht
Haben wir vor einer Reaktion ein sich schnell einstellendes Gleichgewicht, so können wir die Konzentrationen der Produkte dieses Gleichgewichts durch die Gleichgewichtskonstante
$$ K = \frac{\text{Produkte}}{\text{Edukte}} = \frac{k_{\text{hin}}{}}{k_{\text{rück}}} $$
ausdrücken als
$$ [\text{Produkte}] = K \cdot [\text{Edukte}] $$
womit wir bereits eine Variable in unserem System von Gleichungen eliminieren können.
Arrhenius
Das Arrhenius-Gesetz beschreibt die Temperaturabhängigkeit der Geschwindigkeitskonstanten. Es lautet
$$ k(T) = A \exp \left( - \frac{E_A}{R T} \right) $$
wobei $A$ der präexponentielle Faktor und $E_A$ die Aktivierungsenergie ist. Die Aktivierungsenergie $E_A$ ist hier nicht gleich der Schwellenenergie $E_0,$ also der Aktivierungsenergie, wie wir sie in einem Reaktions-Energiediagramm aufzeichnen würden, sondern so definiert, dass die Arrhenius-Gleichung stimmt. Dies gibt uns die Definition
$$ E_A = - R \frac{\partial \ln k}{\partial \frac{1}{T}} $$
womit die Aktivierungsenergie nach Arrhenius eine rein empirische Konstante ist IUPAC Green Book [Seite 64].
Wann sind Aktivierungs- und Schwellenenergie annäherungsweise gleich? Da die thermische Energie durch $k_B T$ gegeben ist, gilt im Limit $k_B T \ll E_0 \Rightarrow E_0 \approx E_A.$ Weiter findet man in der Praxis in der Regel, dass die Arrhenius Aktivierungsenergie im Hochdruckbereich nahe bei der Schwellenenergie $E_0$ liegt, während sie im Niederdruckbereich oft wesentlich kleiner als $E_0$ ist.
Kinetische Matrix
Ich denke hier ist wenn dann nur die Interpretation des Ergebnisses relevant für die Prüfung, die Berechnung würde viel zu lange dauern.
Betrachten wir ein 2-D Beispiel
$$ \ce{A <=>[$k_1$][$k_2$] B} $$
wobei die kinetische 2-dimensionale kinetische Matrix $K$ die Eigenwerte $\lambda_1, \lambda_2$ habe. Wie können wir die Eigenwerte interpretieren?
Handelt es sich um ein geschlossenes Reaktionsnetzwerk, d.h. es finden keine anderen Reaktionen mit den vorkommenden Stoffen statt, so wird es immer einen Eigenwert $\lambda_1 = 0$ geben. Der Eigenvektor dazu entspricht dann dem Vektor der Gleichgewichts-Konzentrationen, da sich diese nicht mit der Zeit ändern nach der Differentialgleichung
$$ \dd{\vec{c}_{eq}}{t} = \exp(K) \cdot \vec{c}_{eq} \overset{!}{=} 0 $$
wobei $\vec{c}_{eq}$ der Eigenvektor zum Eigenwert $\lambda_1 = 0$ ist und damit $K \vec{c}_{eq} = 0.$
Die nicht-verschwindenden Eigenwerte können wir als verallgemeinerte Geschwindigkeitskonstanten erster Ordnung interpretieren. In diesem Beispiel entspricht $\lambda_2 = k_a + k_b$ gerade der effektiven Geschwindigkeitskonstante, die wir in der Auslenkung aus dem Gleichgewicht gesehen haben (siehe Aufgaben Morgen 1)
$$ \Delta(t) = \Delta_0 \cdot e^{-k_{eff} t} $$
Wir formen also den Vektor der Konzentrationen $\vec{c}$ um, so dass wir den "Mix" aus Konzentrationen erhalten, der dafür sorgt, dass das Geschwindigkeitsgesetz für diesen "Mix" nach erster Ordnung verläuft und somit die Lösung $\propto e^{-\lambda_2 t}$ hat.
Ein Beispiel für ein offenes (also nicht geschlossenes) Reaktionsnetzwerk wäre
$$ \ce{A <=>[$k_1$][$k_2$] B ->[$k_3$] P} $$
wobei wir nur die Reaktionen mit den Edukten $\ce{A}$ und $\ce{B}$ betrachten. Hier wird es keinen Eigenwert $\lambda_1 = 0$ geben, da die Konzentrationen der Zwischenprodukte sich nicht einstellen können, da sie weiterreagieren. Den Eigenwert $\lambda_1 = 0$ würden wir bekommen, wenn wir das Produkt $\ce{P}$ auch miteinbeziehen würden und dieser würde dem stationären Zustand, dass nur noch $\ce{P}$ vorhanden ist, entsprechen.
Kettenreaktionen
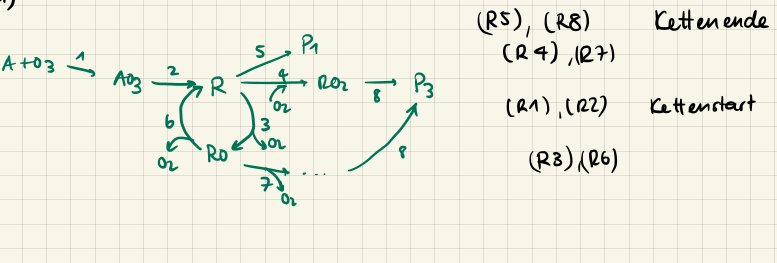
Um bei den Kettenreaktionen die einzelnen Schritte zu identifizieren, ist es hilfreich, das Reaktionsnetzwerk in einem Graphen aufzuzeichnen. Meist (wenn die Prüfungsschreibenden nicht gerade gemein sind) gehört die erste Reaktion dem Kettenstart an. Wir starten also mal bei dieser und folgen dem Weg der Produkte. Irgendwann werden wir auf ein Zwischenprodukt stossen, welches wir schonmal gesehen haben. Der darin eingeschlossene Kreis ist dann die Kette. Reaktionen, die etwas in die Kette einspeisen gehören zum Kettenstart und Reaktionen, die aus der Kette herausgehen gehören zum Kettenabbruch.
Allfällige Hemmungen/Inhibitoren erkennen wir dadurch, dass sie die Kettenreaktion verlangsamen.
Michaelis Menten
Die Geschwindigkeitsgesetze der verschiedenen Formen von Hemmung durch einen Inhibitor sind nochmal schön (in konsistenter Notation) auf einem Formelblatt (siehe Polybox) zusammengefasst. Die Herleitung empfehle ich einfach auf einer ausgedruckten Zusammenfassung dabei zu haben.